Законы движения и взаимной зависимости планет Солнечной системы.

Аннотация. Статья посвящена законам движения и взаимной зависимости планет Солнечной системы происходящих от термодинамических процессов возникающих внутри нашей Вселенной. После открытия нового закона тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) и нового закона тяготения между двумя материальными телами, находящихся в пространстве Солнечной (или другой) системы к центральной звезде Солнцу, можно обосновать некоторые механизмы взаимодействия планет Солнечной системы с Солнцем. Данные аргументы подтверждены новым законом энергии между двумя материальными телами, находящимися в пространстве Солнечной (или другой) системы и нового закона энергии одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде Солнцу. Новый закон активности материального тела находящегося в пространстве даст возможность детально разобраться в самом механизме вращения планет Солнечной системы по эллиптической орбите и по-новому взглянуть на это явление природы.

Из разнообразных противоречивых гипотез строения атома необходимо выделить только планетарную модель строения атома, которая поддаётся логическому осмыслению и её можно доказать вновь открытыми законами физики. Планетарная модель строения атома была предложена Эрнстом Резерфордом. Он в 1911 году, в июньском номере журнала «Philosophical Magazine» опубликовал эту работу по рассеиванию α- и β-частиц веществом и строение атома, в которой он впервые ввел такое понятие как «атомное ядро» и «планетарная модель строения атома». Недостатком планетарной модели была невозможность объяснения данной гипотезы устойчивости атомов. После открытия новых законов образования планет и галактик нашей Вселенной данное научное предположение легко подтвердить новыми доводами. Для наглядности рассмотрим планетарную модель Солнечной системы и взаимодействие всех её планет с Солнцем, по новым законам образования планет и галактик нашей Вселенной.

По закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) можно определить силы тяготения всех планет Солнечной системы к Солнцу, который можно сформулировать так:

Сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) равна произведению массы измеряемого материального тела на модуль ускорения свободного падения измеряемого материального тела, на диаметр измеряемого материального тела, и обратно пропорциональна расстоянию от поверхности Солнца до поверхности измеряемого материального тела.

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности измеряемого материального тела, м

g и - модуль ускорения свободного падения измеряемого материального тела, м/c²

D и - диаметр измеряемого материального тела, м

m и - масса измеряемого материального тела, кг.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Меркурия к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Меркурия = 57910000000 м

g и - модуль ускорения свободного падения планеты Меркурия = 3,70 м/c²

m и - масса планеты Меркурия = 3,330228 ∙ 10²³ кг

D и - диаметр планеты Меркурия = 4879400 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Венеры к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Венеры = 108000000000 м

g и - модуль ускорения свободного падения планеты Венеры = 8,87 м/c²

m и - масса планеты Венеры = 4,8685 ∙ 10²⁴ кг

D и - диаметр планеты Венеры = 12103000 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) определим силу тяготения планеты Земля, к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000000000 м

g и - модуль ускорения свободного падения планеты Земля = 9,80665 м/c²

m и - масса планеты Земля = 5,9726 ∙ 10²⁴ кг

D и - диаметр планеты Земля = 12756200 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Марса к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Марса = 228000000000 м

g и - модуль ускорения свободного падения планеты Марса = 3,711 м/c²

m и - масса планеты Марса = 6,4185 ∙ 10²³ кг

D и - диаметр планеты Марса = 6792400 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения карликовой планеты Церера к центральной звезде (Солнцу), которая расположена в поясе астероидов.

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности карликовой планеты Церера = 413900000000 м

g и - модуль ускорения свободного падения карликовой планеты Церера = 0,27 м/c²

m и - масса карликовой планеты Церера = 9,43 ∙ 10²⁰ кг

D и - диаметр карликовой планеты Церера = 974600 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Юпитера к центральной звезде (Солнцу), которая относится к планетам газовым гигантам.

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Юпитера = 778000000000 м

g и - модуль ускорения свободного падения планеты Юпитера = 24,79 м/c²

m и - масса планеты Юпитера = 1,8986 ∙ 10²⁷ кг

D и - диаметр планеты Юпитера = 142984000 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Сатурна к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Сатурна = 1427000000000 м

g и - модуль ускорения свободного падения планеты Сатурна = 10,44 м/c²

m и - масса планеты Сатурна = 5,6846 ∙ 10²⁶ кг

D и - диаметр планеты Сатурна = 120536000 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Урана к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Урана = 2886000000000 м

g и - модуль ускорения свободного падения планеты Урана = 8,87 м/c²

m и - масса планеты Урана = 8,6832 ∙ 10²⁵ кг

D и – диаметр планеты Урана = 51118000 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Нептуна к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Нептуна = 4498000000000 м

g и - модуль ускорения свободного падения планеты Нептуна = 11,15 м/c²

m и - масса планеты Нептуна = 1,0243 ∙ 10²⁶ кг

D и - диаметр планеты Нептуна = 49528000 м.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим силу тяготения планеты Плутона к центральной звезде (Солнцу).

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Плутона = 5929000000000 м

g и - модуль ускорения свободного падения планеты Плутона = 0,58 м/c²

m и - масса планеты Плутона = 1,305 ∙ 10²² кг

D и – диаметр планеты Плутона = 2374000 м.

Необходимо особо отметить, что не только силы тяготения каждого независимого материального тела находящегося в пространстве Солнечной (или другой) системы взаимодействуют с Солнцем. Вместе с этим и энергия каждого независимого материального тела находящегося в пространстве Солнечной (или другой) системы, тоже взаимодействует с Солнцем.

По закону энергии одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу) можно определить энергию всех планет Солнечной системы к Солнцу, который можно сформулировать так:

Энергия одного материального тела находящегося в пространстве Солнечной (или другой) системы равна произведению массы измеряемого материального тела, на ускорение свободного падения измеряемого материального тела расположенного в пространстве на квадрат расстояния от поверхности центральной звезды (Солнца) до поверхности измеряемого материального тела расположенного в пространстве и обратно пропорциональна произведению диаметра измеряемого материального тела на время взаимодействия между материальными телами.

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности измеряемого материального тела находящегося в пространстве, м

g и - модуль ускорения свободного падения измеряемого материального тела находящегося в пространстве, м/c²

D и - диаметр измеряемого материального тела расположенного в пространстве, м

m и - масса измеряемого материального тела расположенного в пространстве, кг

t – время взаимодействия между материальными телами, с.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Меркурия к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Меркурия = 57910000000 м

g и - модуль ускорения свободного падения планеты Меркурия = 3,70 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Меркурия = 3,330228 ∙ 10²³ кг

D и - диаметр планеты Меркурия = 4879400 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Венера к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Венера = 108000000000 м

g и - модуль ускорения свободного падения планеты Венера = 8,87 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Венера = 4,8685 ∙ 10²⁴ кг

D и - диаметр планеты Венера = 12103000 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Земля к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000000000 м

g и - модуль ускорения свободного падения планеты Земля = 9,8 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Земля = 5,9726 ∙ 10²⁴ кг

D и - диаметр планеты Земля = 12756200 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Марса к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Марса = 228000000000 м

g и - модуль ускорения свободного падения планеты Марса = 3,711 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Марса = 6,4185 ∙ 10²³ кг

D и - диаметр планеты Марса = 6792400 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию карликовой планеты Церера к центральной звезде (Солнцу), которая расположена в поясе астероидов.

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности карликовой планеты Церера = 413900000000 м

g и - модуль ускорения свободного падения карликовой планеты Церера = 0,27 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса карликовой планеты Церера = 9,43 ∙ 10²⁰ кг

D и - диаметр карликовой планеты Церера = 974600 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Юпитера к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Юпитера = 778000000000 м

g и - модуль ускорения свободного падения планеты Юпитера = 24,79 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Юпитера = 1,8986 ∙ 10²⁷ кг

D и - диаметр планеты Юпитера = 142984000 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Сатурна к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Сатурна = 1427000000000 м

g и - модуль ускорения свободного падения планеты Сатурна = 10,44 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Сатурна = 5,6846 ∙ 10²⁶ кг

D и - диаметр планеты Сатурна = 120536000 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Урана к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Уран = 2886000000000 м

g и - модуль ускорения свободного падения планеты Урана = 8,87 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса материального тела планеты Урана = 8,6832 ∙ 10²⁵ кг

D и - диаметр материального тела планеты Урана = 51118000 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Нептуна к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Нептуна = 4498000000000 м

g и - модуль ускорения свободного падения планеты Нептуна = 11,15 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Нептуна = 1,0243 ∙ 10²⁶ кг

D и - диаметр планеты Нептуна = 49528000 м.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Плутона к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Плутона = 5929000000000 м

g и - модуль ускорения свободного падения планеты Плутона = 0,58 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Плутона = 1,305 ∙ 10²² кг

D и - диаметр планеты Плутона = 2374000 м.

После вычисления сил тяготения и энергии каждой планеты Солнечной системы к Солнцу, сведём все расчёты в таблицу № 1. Из некоторых физических характеристик планет Солнечной системы становится ясно, что в зависимости от активности планет и её расположение в пространстве меняется не только сила тяготения, но и энергия этих планет. Здесь легко заметить разницу, с которой происходит изменение сил тяготения и энергии каждой планеты.

Таблица № 1

1. – Ускорение свободного падения планет Солнечной системы, м/c².

2. – Сила тяготения планет Солнечной системы к центральной звезде Солнцу, Н.

3. – Энергии планет Солнечной системы к центральной звезде Солнцу, Вт.

4. – Количество спутников каждой планеты Солнечной системы, шт.

5. – Масса планет Солнечной системы, кг.

6. – Диаметр планет Солнечной системы, м.

В оранжевом поясе астероидов расположены обломки планет или планеты обладающие малой активностью, которые аналогичны планете Церера.

Необходимо обратить особое внимание на пояс астероидов, где сила тяготения одной малой планеты Церера очень маленькая к центральной звезде к Солнцу, но их количество очень большое. Данное явление природы, происходящее в поясе астероидов, где от большого количества астероидов возникает большая сила тяготения и большой энергетический заряд, который притягивает к себе даже такую гигантскую планету как Юпитер.

Однако этими связями сил тяготения и энергии каждой планеты Солнечной системы не ограничиваются. Существуют силы тяготения и энергии между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы.

По закону тяготения между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы можно определить силу тяготения между двумя материальными телами в пространстве Солнечной (или другой) системы. Этот закон можно сформулировать так:

Сила тяготения между двумя материальными телами находящихся в пространстве Солнечной (или другой) системы равна сумме произведения массы первого материального тела на модуль ускорения свободного падения первого материального тела, произведения массы второго материального тела на модуль ускорения свободного падения второго материального тела и произведению квадрата расстояния от поверхности первого материального тела до поверхности второго материального тела, и обратно пропорциональна произведению расстояния от поверхности Солнца до поверхности первого материального тела и расстояния от поверхности Солнца до поверхности второго материального тела.

где:

F тс - сила тяготения между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы, Н

L м - расстояние от поверхности первого материального тела до поверхности второго материального тела, м

L с1 - расстояние от поверхности Солнца до поверхности первого материального тела, м

L с2 - расстояние от поверхности Солнца до поверхности второго материального тела, м

g 1 - модуль ускорения свободного падения первого материального тела, м/c²

g 2 - модуль ускорения свободного падения второго материального тела, м/c²

m 1 - масса первого материального тела, кг

m 2 - масса второго материального тела, кг.

Например, по новому закону тяготения между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы можно определить силу тяготения планеты Земля к планете Венера. При этом необходимо учесть, что Венера - самая близкая к Земле планета Солнечной системы. Однако расстояние от Земли до Венеры постоянно меняется потому, что обе планеты движутся по круговым орбитам вокруг Солнца с разной скоростью. Так, Венера делает полный круг вокруг Солнца за 224,7 дня, тогда как Земля - за 365,26, поэтому их максимальные сближения и удаления повторяются лишь каждые 584 дня. Минимальное расстояние от Земли до Венеры во время их сближения составляет - 40 млн. км., а максимальное расстояние во время их удаления составляет - 260 млн. км.

Например, по закону тяготения между двумя материальными телами, которые находятся в пространстве Солнечной системы, определим силу тяготения между планетой Венера и планетой Земля во время их максимального сближения и во время их максимального удаления.

где:

F тс - сила тяготения между двумя материальными телами находящихся в пространстве Солнечной (или другой) системы, Н

L м - расстояние от поверхности планеты Венера до поверхности планеты Земля во время их максимального сближения = 40000000000 м

L м - расстояние от поверхности планеты Венера до поверхности планеты Земля во время их максимального удаления = 260000000000 м

L с1 - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Венера = 108000000000 м

L с2 - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000000000 м

g 1 - модуль ускорения свободного падения планеты Венера = 8,87 м/c²

g 2 - модуль ускорения свободного падения планеты Земля = 9,80665 м/c²

m1 - масса планеты Венера = 4,8685 ∙ 10²⁴ кг

m 2 - масса планеты Земля = 5,9726 ∙ 10²⁴ кг.

Из произведённых расчётов необходимо сделать вывод, что планета Венера и планета Земля взаимодействуют между собой по силе не только во время их максимального сближения или их максимального удаления, но и с другими планетами Солнечной системы и Солнцем. Таким взаимодействием между собой обладают не только активные планеты, но и пассивные планеты (астероиды), которые взаимодействуют между собой на разных уровнях, образуя саморегулирующуюся замкнутую энергетическую систему. Необходимо особо отметить, что сила тяготения между планетой Венера и планетой Земля больше чем сила тяготения каждой из этих планет с Солнцем.

По закону энергии между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы можно определить энергию между двумя материальными телами в пространстве Солнечной (или другой) системы. Этот закон можно сформулировать так:

Энергия между двумя материальными телами, находящимися в пространстве Солнечной (или другой) системы равна сумме произведений массы первого материального тела на модуль ускорения свободного падения первого материального тела и массы второго материального тела на модуль ускорения свободного падения второго материального тела расположенного в пространстве на квадрат расстояния от первого материального тела до второго материального тела находящегося в пространстве и обратно пропорционально произведению расстояния от поверхности центральной звезды (Солнца) до поверхности первого материального тела и от поверхности центральной звезды (Солнца) до поверхности второго материального тела находящегося в пространстве и времени взаимодействия между материальными телами.

где:

Е дмт - энергия между двумя материальными телами находящихся в пространстве Солнечной (или другой) системы, Вт

L1- расстояние от поверхности центральной звезды (Солнца) до поверхности первого материального тела находящегося в пространстве, м

L2 - расстояние от поверхности центральной звезды (Солнца) до поверхности второго материального тела находящегося в пространстве, м

g 1 - модуль ускорения свободного падения первого материального тела находящегося в пространстве, м/c²

g 2 - модуль ускорения свободного падения второго материального тела находящегося в пространстве, м/c²

L - расстояние от первого материального тела до второго материального тела находящегося в пространстве, м

m 1 - масса первого материального тела расположенного в пространстве, кг

m 2 - масса второго материального тела расположенного в пространстве, кг

t – время взаимодействия между материальными телами, с.

Например, по закону энергии между двумя материальными телами, которые находятся в пространстве Солнечной системы, определим энергию между планетой Венера и планетой Земля во время их максимального сближения и во время их максимального удаления.

где:

F тс - сила тяготения между двумя материальными телами находящихся в пространстве Солнечной (или другой) системы, Н

L м - расстояние от поверхности планеты Венера до поверхности планеты Земля во время их максимального сближения = 40000000000 м

L м - расстояние от поверхности планеты Венера до поверхности планеты Земля во время их максимального удаления = 260000000000 м

L с 1 - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Венера = 108000000000 м

L с 2 - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000000000 м

g 1 - модуль ускорения свободного падения планеты Венера = 8,87 м/c²

g 2 - модуль ускорения свободного падения планеты Земля = 9,80665 м/c²

m 1 - масса планеты Венера = 4,8685 ∙ 10²⁴ кг

m 2 - масса планеты Земли = 5,9726 ∙ 10²⁴ кг.

Из произведённых расчётов необходимо сделать вывод, что планета Венера и планета Земля взаимодействуют между собой не только во время их максимального сближения или их максимального удаления, но и с другими планетами Солнечной системы и Солнцем. Таким взаимодействием между собой обладают не только активные планеты, но и пассивные планеты (астероиды), которые взаимодействуют между собой на разных уровнях, образуя саморегулирующуюся замкнутую энергетическую систему. Необходимо особо отметить, что энергия между планетой Венера и планетой Земля меньше чем энергия каждой из этих планет к Солнцу.

Например, по закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) определим силу тяготения планеты Земля, которая по каким-либо причинам утратила ускорение свободного падения тел в пространстве.

где:

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), Н

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000000000 м

g и - модуль ускорения свободного падения планеты Земля = 0,00 м/c²

m и - масса планеты Земля = 5,9726 ∙ 10²⁴ кг

D и - диаметр планеты Земля = 12756200 м.

Необходимо отметить, что если планета Земля по каким-либо причинам из активного состояния перейдёт в пассивное состояние и потеряет ускорение свободного падения тел в пространстве, то она может немного изменить своё расположение в пространстве, но останется на своей орбите. Подтвердим это явление природы на конкретном примере, когда планета Земля по каким-либо причинам потеряла свою активность.

По закону тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) определим расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля при утрате ей ускорения свободного падения тел в пространстве.

где:

Lс - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля, м

F тсо - сила тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) = 5,079178 ∙ 10²⁰ Н

g и - модуль ускорения свободного падения планеты Земля = 0,00 м/c²

m и - масса планеты Земли = 5,9726 ∙ 10²⁴ кг

D и - диаметр планеты Земля = 12756200 м.

После произведённых расчётов определим, на какое расстояние сместится планета Земля при потере ускорения свободного падения тел в пространстве.

Необходимо установить чёткое правило, что под активностью необходимо понимать явление природы, при котором ускорение свободного падения тел в пространстве на планетах Солнечной (или другой) системы превышает 1 м/с², то тогда можно будет считать, что это активная планета. Если ускорение свободного падения тел в пространстве на планете не будет превышать 1 м/с², то можно будет считать что это пассивная планета или астероид.

Например, по закону энергии одного материального тела расположенного в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу), определим энергию планеты Земля, которая по каким-либо причинам утратила ускорение свободного падения тел в пространстве, к центральной звезде (Солнцу).

где:

Е oмт - энергия одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу), Вт

L - расстояние от поверхности центральной звезды (Солнца) до поверхности планеты Земля = 150000019924 м

g и - модуль ускорения свободного падения планеты Земля = 0,00 м/c²

t - время взаимодействия между материальными телами = 1 с

m и - масса планеты Земля = 5,9726 ∙ 10²⁴ кг

D и - диаметр планеты Земля = 12756200 м.

Из произведённых расчётов видно, что планета Земля, которая по каким-либо причинам утратила ускорение свободного падения тел в пространстве, потеряла часть своей энергии, но продолжит находиться на своей орбите внутри Солнечной системы. При этом замкнутая энергетическая система немного изменит свою конфигурацию. Данный факт неоспоримо доказывает, что не только активные, но и пассивные планеты или астероиды при изменении энергии продолжат находиться внутри Солнечной системы.

Законы энергии тесно связаны с законом тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу) и законом тяготения между двумя материальными телами, находящихся в пространстве Солнечной (или другой) системы и новым законом ускорения свободного падения тел в пространстве. При изменении положения одного материального тела расположенного в пространстве по отношению к другому материальному телу будет меняться не только тяготение этого материального тела, но и его энергия, что можно наглядно посмотреть на конкретных примерах.

Необходимо особо подчеркнуть, что сила тяготения между двумя материальными телами расположенных в пространстве сильно влияет на энергию этих материальных тел. При увеличении силы тяготения между двумя материальными телами расположенных в пространстве уменьшается их энергия. При уменьшении силы тяготения между двумя материальными телами расположенных в пространстве увеличивается их энергия.

Необходимо учесть, что из-за взаимодействия всех сил тяготения и энергии между материальными телами расположенных в пространстве, активная планета Земля должна двигаться по своей орбите с небольшим волновым перемещением.

Например, возьмём для исследования первую четверть Луны поз. 3, которая расположена на одной оси вращения активной планеты Земля у которой:

– Сила тяготения Луны к Земле = 193781701941145225075,1816282735 Н.

– Сила тяготения Луны к Солнцу = 2766999285159928041,478267377677 Н.

– Энергия Луны к Земле = 387192985897327138423,4409781055 Вт.

– Энергия Луны к Солнцу = 1,075751938412883535811759095307 ∙ 10³⁶ Вт.

Например, возьмём для исследования пассивный спутник Луну, находящуюся в перигее, поз. 4, к активной планете Земля у которой:

– Сила тяготения Луны к Земле = 194290130182817634928,1765011283 Н.

– Сила тяготения Луны к Солнцу = 2774259106738386219,977397144565 Н.

– Энергия Луны к Земле = 388208870508906501486,7406862366 Вт.

– Энергия Луны к Солнцу = 1,070107041129208327599364666751 ∙ 10³⁶ Вт

Например, возьмём для исследования последнюю четверть Луны поз. 5, которая расположена на одной оси вращения активной планеты Земля у которой:

– Сила тяготения Луны к Земле = 193781701941145225075,1816282735 Н.

– Сила тяготения Луны к Солнцу = 2766999285159928041,478267377677 Н.

– Энергия Луны к Земле = 387192985897327138423,4409781055 Вт.

– Энергия Луны к Солнцу = 1,075751938412883535811759095307 ∙ 10³⁶ Вт.

Например, возьмём для исследования пассивный спутник Луну, находящуюся в апогее, поз. 6, к активной планете Земля у которой:

– Сила тяготения Луны к Земле = 193273273699472815222,1867554188 Н.

– Сила тяготения Луны к Солнцу = 2759739463581469862,979137610789 Н.

– Энергия Луны к Земле = 386177101285747775360,1412699745 Вт.

– Энергия Луны к Солнцу = 1,081396835696558744024153523864 ∙ 10³⁶ Вт.

Для наглядности рассмотрим схематическое изображение взаимодействия всех сил тяготения и энергии Луны, спутника планеты Земля, которая перемещается по эллиптической орбите, фиг.1.

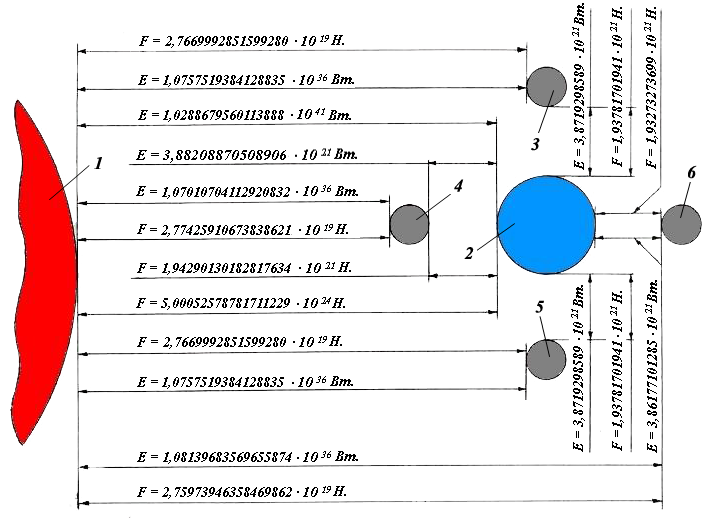
Фиг.1

где:

Поз. 1 – Солнце.

Поз. 2 – Земля.

Поз. 3 – Первая четверть Луны расположенная на одной оси вращения Земли.

Поз. 4 – Полнолуние Луны находящейся в перигее.

Поз. 5 – Последняя четверть Луны расположенная на одной оси вращения Земли.

Поз. 6 – Новолуние Луны находящейся в апогее.

Необходимо учитывать, что эти показания нужно интегрировать с тяготением Земли к Солнцу и энергией Земли к Солнцу. Для более точных математических расчётов необходимо ещё принять во внимание все планеты Солнечной системы.

Тяготение Земли к Солнцу = 500052578781711229946541,24064171121 Н

Энергия Земли к Солнцу = 1,0288679560113888645001066138197 ∙ 10⁴¹ Вт

На фиг.1 видно, что все силы тяготения материальных тел расположенных в пространстве и их энергия взаимодействуют только в движении, что наглядно подтверждено новыми законами физики.

Новый закон силы взаимодействия двух точечных зарядов расположенных в вакууме можно сформулировать так:

Сила взаимодействия двух точечных зарядов расположенных в вакууме прямо пропорциональна сумме произведений массы первого заряда на скорость его перемещения в вакууме и произведения массы второго заряда на скорость его перемещения в вакууме и обратно пропорциональна времени взаимодействия точечных зарядов.

где:

F_q - сила взаимодействия двух точечных зарядов расположенных в вакууме, Н

- скорость перемещения заряда в вакууме, м/с

t - время взаимодействия точечных зарядов, с

m₁ - масса первого точечного заряда, кг

m₂ - масса второго точечного заряда, кг.

Более подробная информация с конкретными примерами и доказательными фактами новых законов и механизмов образования планет Солнечной системы и галактик нашей Вселенной хорошо изложена в материалах заявок на изобретения  № 2005129781 от 28 сентября 2005 года и  № 2005140396 от 26 декабря 2005 года.

В заключении можно сказать, что наш материальный мир очень многообразен и все процессы, совершаемые в нём от случайно сложившихся обстоятельств, которые происходят во времени, в разной мере, влияют один на другой, поэтому выдвигается новая теория многогранной зависимости. В этом мире всё переплетено, и одно явление природы в разной мере находятся в зависимости к другому. Более активные материальные тела доминируют над менее активными материальными телами, поэтому не может быть постоянных констант, законов или физических величин. Например, новый закон тяготения между двумя материальными телами, которые расположены в пространстве Солнечной (или другой) системы тесно связан с новым законом тяготения одного материального тела находящегося в пространстве Солнечной (или другой) системы к центральной звезде (Солнцу). В тоже время законы тяготения находятся в постоянной зависимости от нового закона активности материального тела расположенного в пространстве и нового закона ускорения свободного падения тел в пространстве. А перечисленные законы тесно связаны с новым законом энергии между двумя материальными телами, которые находятся в пространстве Солнечной (или другой) системы и новым законом энергии одного материального тела, находящегося в пространстве Солнечной (или другой) системы, к центральной звезде (Солнцу) и многим другим...